楽譜について学ぶ
第3日 音程
今回からは音楽における基本的な原理や成り立ちについて学びます。また、今回は『音程』について学びます。『音と音とのへだたりをどう測るか?』・・・これが音程というものです。音程はメロディーや和音を理解するときなどにも使われます。
次の基礎知識をしっかりマスターしましょう。
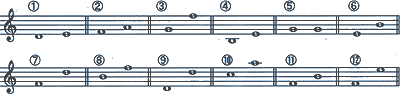
音程基礎知識

1)
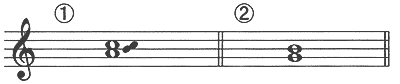
この2つの音のへだたりは、同じように見えますが、
2)
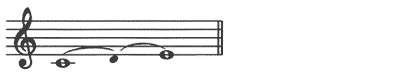
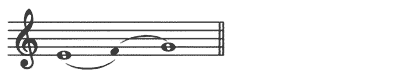
だから
1. 音程
音程とは、2音間の音のへだたりをいい、それを度数で表わします。
度数

a) は、同じ音どうしなので、音のへだたりはありません。これを1度(同度)といいます。
b) は、隣り合った音で2度となります。
c) は、ミから数えて、ドの音は6個目です。ですから6度です。
度数はこのように判断していくのです。
度数

a) は、同じ音どうしなので、音のへだたりはありません。これを1度(同度)といいます。
b) は、隣り合った音で2度となります。
c) は、ミから数えて、ドの音は6個目です。ですから6度です。
度数はこのように判断していくのです。
2. 幹音間の音程
シャープやフラットの付かない音を幹音といいましたね。この幹音間の音程は、完全系の度数と、長短系の度数の2通りに分かれます。
1) 完全系の音程
1、4、5、8度が完全系の度数です。
a) 1度と8度

・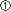 と
と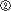 は、同度で完全1度といいます。
は、同度で完全1度といいます。
・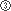 と
と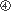 は、8度で完全8度といいます。
は、8度で完全8度といいます。
b) 5度

・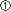 から
から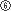 までの5度は、半音を必ず1個含んでいます。これらを完全5度といいます。
までの5度は、半音を必ず1個含んでいます。これらを完全5度といいます。
・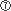 は2個の半音を含んでいるので、完全5度より音の幅は狭くなっています。これを減5度といいます。
は2個の半音を含んでいるので、完全5度より音の幅は狭くなっています。これを減5度といいます。
c) 4度

・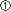 、
、
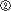 、
、
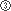 、
、
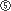 、
、
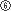 、
、
 の音程には、半音が必ず1個含まれています。これらの音程を完全4度といいます。
の音程には、半音が必ず1個含まれています。これらの音程を完全4度といいます。
・ の音程には半音が含まれていません。これを増4度といいます。
の音程には半音が含まれていません。これを増4度といいます。
以上が完全系の音程です。音程の基礎知識を基に考えればよく分かりますね。 完全という言葉の意味は、よく協和して響き合うということです。同じ5度でも完全と減とでは全く違う響きになります。ですから、必ず音を出して聴き較べて下さい。
2) 長短系の音程
完全系以外の2、3、6、7度が長短系の音程です。
a) 2度

・ は全音で、長2度となります。
は全音で、長2度となります。
・ は半音で、短2度です。短2度はこのミ ファとシ ドの2つだけです。
は半音で、短2度です。短2度はこのミ ファとシ ドの2つだけです。
b) 3度

・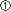 には半音が1個、
には半音が1個、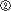 には半音がありません。
には半音がありません。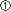 は短3度、
は短3度、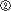 は長3度です。
は長3度です。
・半音を含まない3度が長で、半音1個が短です。
c) 6度

・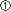 には半音が1個、
には半音が1個、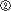 は半音が2個ですね。当然
は半音が2個ですね。当然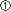 が
が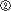 より音のへだたりが半音分長いです。
より音のへだたりが半音分長いです。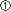 は長6度、
は長6度、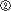 は短6度です。
は短6度です。
・半音数1個が長で、2個が短です。
d) 7度

・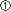 には半音が1個、
には半音が1個、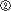 は半音が2個ですね。
は半音が2個ですね。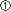 は長7度、
は長7度、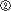 は短7度です。
は短7度です。
・6度と同じで、半音1個で長、半音2個で短です。
以上1オクターヴ内の幹音間の音程についてみてきました。これを簡単な表にまとめてみましょう。
音程の種別表
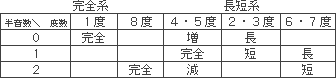
1) 完全系の音程
1、4、5、8度が完全系の度数です。
a) 1度と8度

・
・
b) 5度

・
・
c) 4度

・
・
以上が完全系の音程です。音程の基礎知識を基に考えればよく分かりますね。 完全という言葉の意味は、よく協和して響き合うということです。同じ5度でも完全と減とでは全く違う響きになります。ですから、必ず音を出して聴き較べて下さい。
2) 長短系の音程
完全系以外の2、3、6、7度が長短系の音程です。
a) 2度

・
・
b) 3度

・
・半音を含まない3度が長で、半音1個が短です。
c) 6度

・
・半音数1個が長で、2個が短です。
d) 7度

・
・6度と同じで、半音1個で長、半音2個で短です。
以上1オクターヴ内の幹音間の音程についてみてきました。これを簡単な表にまとめてみましょう。
音程の種別表

【例題1】
次の2音間の音程を答えよ。
<解説>
<答え> 短6度
<答え> 完全4度
3. 派生音を含む音程
音程の移動図
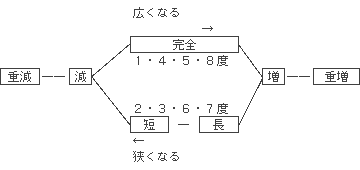
上図は、各音程の種類が半音関係で移動する図です。完全系と長短系は、はっきり区別して覚えて下さい。
さて、派生音を含む音程に入りましょう。音程の移動図を用いることで全て解決するはずです。
ここでは例題を基に解説していきましょう。全て2音間の音程を答える例題です。

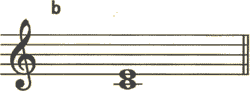
aの音程を解くためには。まず始めにミのフラットを取り除き、幹音間の音程を考えます。
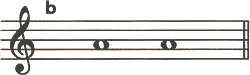
bの音程は長3度です。この長3度を上記の音程の移動図で位置を確認しましょう。aにはミのフラットが付いていますから、bの音程より半音分狭くなります。ですから、音程の移動図は、ひとつ左に移動し、短となります。
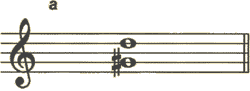
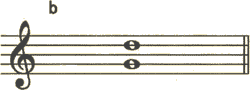
aを幹音間の音程にすると、bの完全5度となります。
b:aのソのシャープで音程の移動図は、半音狭い減に移動します。
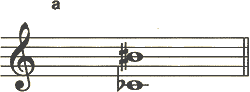
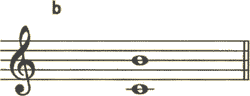
aを幹音間の音程にするとbは長7度です。
下のドの音にフラットをつけると半音広くなり増7度。上のシにシャープがつくと、また半音広くなり重増になります。
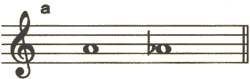

上図は、各音程の種類が半音関係で移動する図です。完全系と長短系は、はっきり区別して覚えて下さい。
さて、派生音を含む音程に入りましょう。音程の移動図を用いることで全て解決するはずです。
ここでは例題を基に解説していきましょう。全て2音間の音程を答える例題です。
【例題1】

<解説>
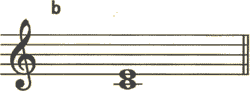
aの音程を解くためには。まず始めにミのフラットを取り除き、幹音間の音程を考えます。
bの音程は長3度です。この長3度を上記の音程の移動図で位置を確認しましょう。aにはミのフラットが付いていますから、bの音程より半音分狭くなります。ですから、音程の移動図は、ひとつ左に移動し、短となります。
<答え> 短3度
【例題2】
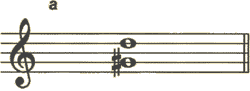
<解説>

aを幹音間の音程にすると、bの完全5度となります。
b:aのソのシャープで音程の移動図は、半音狭い減に移動します。
<答え> 減5度
【例題3】
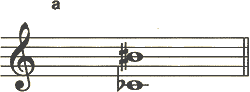
<解説>
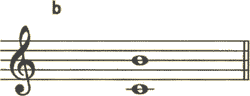
aを幹音間の音程にするとbは長7度です。
下のドの音にフラットをつけると半音広くなり増7度。上のシにシャープがつくと、また半音広くなり重増になります。
<答え> 重増7度
【例題4】
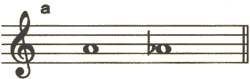
<解説>
幹音間の音程は完全1度です。
b:音程は常に低い音から高い音を見るので、ラのフラットからラの音を見るのです。すると半音上がっていますね。
<答え> 増1度
コラム:派生音を含む音程について
派生音を含む音程は、幹音間の音程にまず直し、音程の移動図を用いて求めれば簡単です。派生音により、音程が広くなっているのか狭くなっているのか、よく気をつけていれば問題ありません。
4. 単音程と複音程
複音程のもとめ方

a) 上記の音程は次の2つに分解することができます。
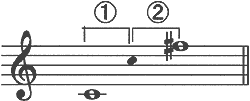
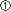 は1オクターヴ、
は1オクターヴ、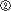 は増4度ですね。答え方は、そのまま、1oct.と増4度となります。
は増4度ですね。答え方は、そのまま、1oct.と増4度となります。
b) もうひとつの答え方は、下のドから上のファのシャープまでの度数を数え、その度数に単音程の増4度の増が付いて、
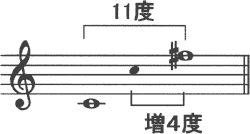
答えは増11度です。
この答え方は音が離れると面倒なので7×oct.数+単音程=複音程を使うと便利です。

a) 上記の音程は次の2つに分解することができます。

b) もうひとつの答え方は、下のドから上のファのシャープまでの度数を数え、その度数に単音程の増4度の増が付いて、

答えは増11度です。
この答え方は音が離れると面倒なので7×oct.数+単音程=複音程を使うと便利です。
5. 転回音程
転回音程は1オクターヴ以内で考えます。

aは低いミの音を1オクターヴ高くすることによってできた音程です。 bは高いソの音を1オクターヴ低くすることによってできた音程です。 音高は違っても、音程は変わりませんね。これが転回音程です。転回音程に対して、始めの音程を原音程といいます。
1 ) 転回音程の度数の求め方
転回音程は、原音程とあわせて、1オクターヴになるので
9-原音程=転回音程
となります。
2 ) 長・単・完全などの種類の変換
完全←→完全
長←→短
増←→減
重増←→重減
1.短6度
2.増4度
2.同じように9-4=5度。増は減になり、答えは減5度です。

aは低いミの音を1オクターヴ高くすることによってできた音程です。 bは高いソの音を1オクターヴ低くすることによってできた音程です。 音高は違っても、音程は変わりませんね。これが転回音程です。転回音程に対して、始めの音程を原音程といいます。
1 ) 転回音程の度数の求め方
転回音程は、原音程とあわせて、1オクターヴになるので
9-原音程=転回音程
となります。
2 ) 長・単・完全などの種類の変換
完全←→完全
長←→短
増←→減
重増←→重減
【例題1】
次の転回音程を答えよ。1.短6度
2.増4度
<解説>
1.転回音程の度数は、9-原音程なので9-6=3度ですね。また、短は長になるので答えは長3度です。2.同じように9-4=5度。増は減になり、答えは減5度です。
6. 協和音程と不協和音程
音程は2音の響き方で、次のように分類されます。
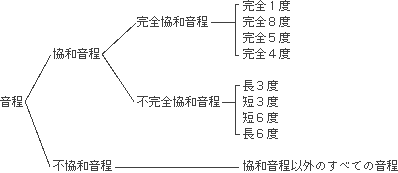

前回(第2日)【問題1】の答え
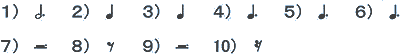
次回は音階について学びます。